Caos, orden y preguntas no resueltas para Pi, el número más importante de las matemáticas

Hoy es el día 14 de marzo, o si lo escribimos en formato numérico, el 3/14. Estas son las tres primeras cifras de uno de los números más célebres, importantes y con más historia de la ciencia. Estamos hablando del número π. Por este motivo hoy es el Día Internacional de las Matemáticas (con una página web muy recomendable). Este año la conmemoración tiene como lema “matemáticas para todo el mundo”, porque para entender el mundo actual todos necesitamos hablar en el lenguaje de las matemáticas. π es una de las piezas clave del lenguaje de las matemáticas y todavía quedan muchas preguntas abiertas sobre este número.

Se ha escrito largo y tendido sobre el número π desde los comienzos de la civilización. Y no es para menos: el mundo, tal y como lo entendemos, depende de manera crítica de esta constante universal. Su definición es bien conocida: si tomamos un círculo cualquiera de diámetro 1, π es la relación entre su longitud y su diámetro. Es independiente del círculo que tomemos: se trata de un invariante geométrico universal. Pese a esta simple definición, expresar el número π de manera explícita es muy complejo. En su expansión decimal no hay patrones numéricos evidentes. La estadística más sencilla que podemos estudiar es el número de apariciones de un dígito dado.

Los resultados experimentales (tomando muchos dígitos en la expansión decimal de π) parecen mostrar que cada dígito aparece un 10% de las ocasiones. Pero esto se trata únicamente de una conjetura: a fecha de hoy es una pregunta abierta saber si para cualquier truncamiento de la expansión decimal de los dígitos de π, la proporción de cada uno de los dígitos es esencialmente la misma.

Más allá de la distribución de los dígitos, otra pregunta interesante de la que se desconoce la respuesta es la siguiente: si tomamos un número cualquiera (por ejemplo, el 44685035261931188171), ¿es cierto que dicho número aparece en la expansión decimal de π? Todos los indicios y experimentos parecen indicar que sí, pero a fecha de hoy no tenemos herramientas matemáticas que permitan responder a esta pregunta de forma general.

De ser cierto el resultado anterior podríamos decir que dentro de π existe todo el conocimiento universal. Es así: si utilizamos un método de codificación numérico para codificar las letras del alfabeto (por ejemplo, si codificamos la letra a mediante 00, la letra b mediante 01, y usamos los dígitos 99 para codificar el espacio en blanco), cualquier libro (escrito o todavía por escribir) se podría codificar con un número muy largo, pero finito. Si cualquier patrón está contenido en la expansión de pi, podríamos encontrar el Quijote, las obras perdidas de Aristóteles y todas las novelas que están por escribir hasta el fin de la humanidad, aun teniendo que tomar un número inimaginable de cifras.

Esto parece señalar que el caos impera en la expansión de π . Sin embargo, lo realmente bello es que existen multitud de expresiones del número π donde reinan el orden y los patrones. Empezando por el producto infinito de Wallis, una fórmula demostrada en el año 1655 que afirma que

.

.

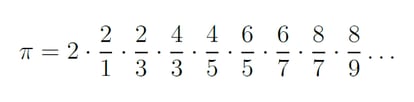
O, con sumas en lugar de productos, la llamada fórmula de Leibniz, deducida en el siglo XVII por el matemático alemán que le da su nombre:

.

.

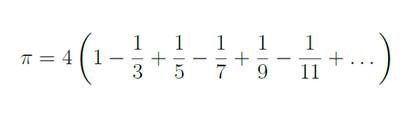
Y, no nos podemos olvidar de la que es quizás la fórmula más importante de las matemáticas, la fórmula de Euler, que relaciona los cinco números más importantes: el 0, el 1, el número π, el número e (la base de los logaritmos neperianos) y la unidad imaginaria i.

Estos son solo tres ejemplos que muestran la ubicuidad del número π en el universo matemático, y que ejemplifican la belleza y la armonía de las matemáticas en un día de celebración para nuestra comunidad.

.

Juanjo Rue es profesor agregat del Departamento de Matemáticas de la Universitat Politècnica de Catalunya (UPC), miembro del Instituto de Matemáticas de la UPC (IMTech) e investigador adscrito al Centre de Recerca Matemàtica (CRM).

.

Ágata Timón G Longoria es coordinadora de la Unidad de Cultura Matemática del ICMAT

.

Café y Teoremas es una sección dedicada a las matemáticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matemáticas (ICMAT), en la que los investigadores y miembros del centro describen los últimos avances de esta disciplina, comparten puntos de encuentro entre las matemáticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar café en teoremas. El nombre evoca la definición del matemático húngaro Alfred Rényi: “Un matemático es una máquina que transforma café en teoremas”.

.

Edición y coordinación: Ágata A. Timón G Longoria (ICMAT).

.

.

· Link

.

.

.

.